Problem - Leetcode

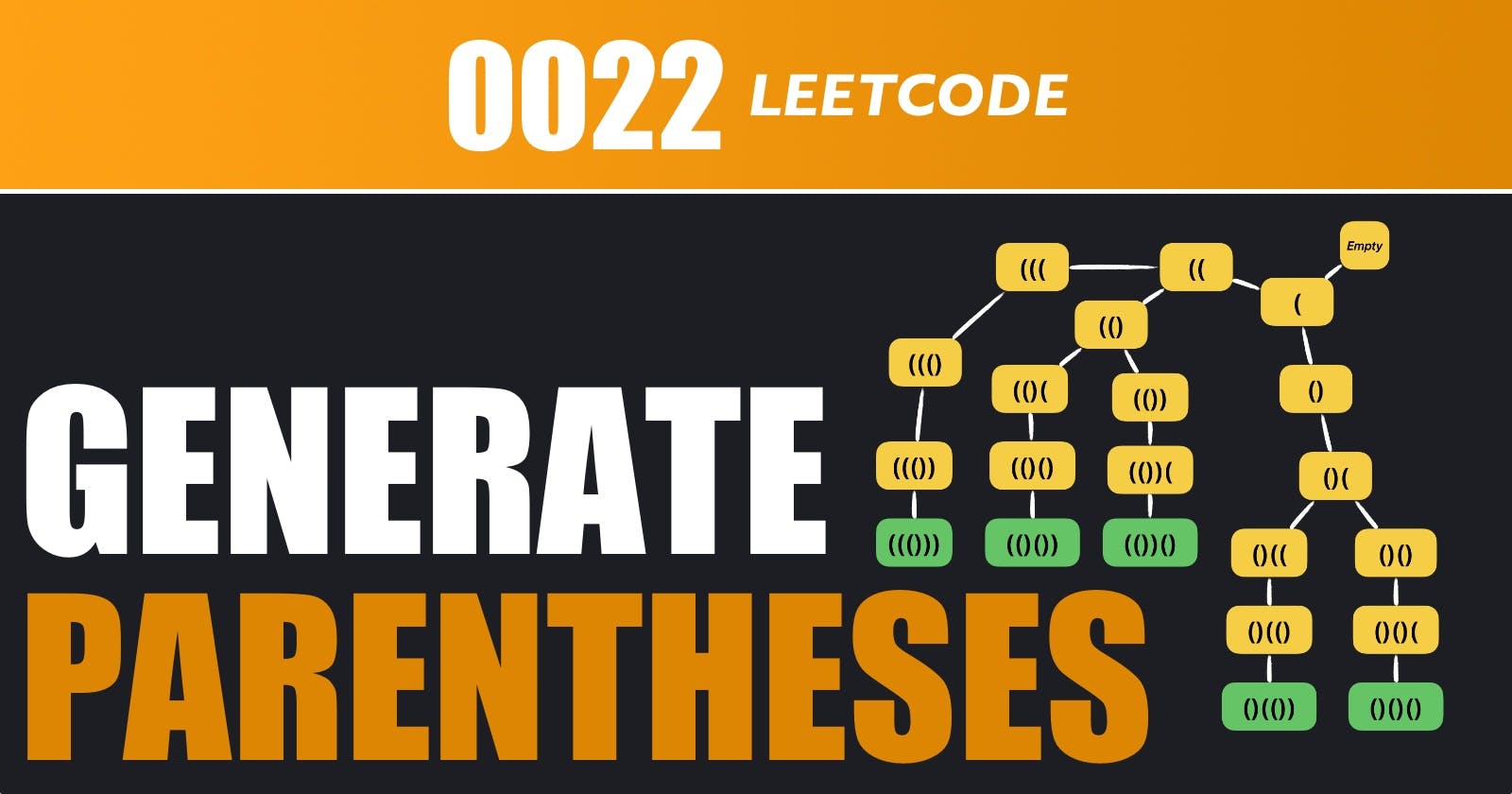
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

Example 1:

Input: n = 3
Output: ["((()))","(()())","(())()","()(())","()()()"]

Example 2:

Input: n = 1
Output: ["()"]

Constraints:

• 1 <= n <= 8

Solution in Golang

import "strings"
func generateParenthesis(n int) []string {
    var stack []string
    var res []string
    var backtrack func(int, int)
    backtrack = func(openN int, closedN int){
      if openN == n && closedN == n && openN == closedN{
        res = append(res, strings.Join(stack, ""))
        return
      }
      if openN < n{
        stack = append(stack, "(")
        backtrack(openN+1, closedN)
        pop(&stack)
      }
      if closedN < openN{
        stack = append(stack, ")")
        backtrack(openN, closedN+1)
        pop(&stack)
      }
    }
    backtrack(0,0)
    return res
}

func pop(list *[]string){
  length := len(*list)
  *list = (*list)[:length-1]
}

This Go code defines a function generateParenthesis that generates all valid combinations of parentheses pairs with a given number n. Here's a detailed explanation of the code:

1. import "strings": This line imports the "strings" package, which is used for manipulating strings, particularly to join them together.

2. func generateParenthesis(n int) []string { ... }: This is the main function that takes an integer n as input and returns a slice of strings representing valid combinations of parentheses.

3. Inside this function, three main variables are defined:

   • stack []string: A slice of strings used to keep track of the currently open and unclosed parentheses.

   • res []string: A slice of strings to store the final result, i.e., valid combinations of parentheses.

   • backtrack func(int, int): This is a nested function that performs the recursive backtracking to generate the combinations.

4. backtrack is a recursive function that takes two arguments:

   • openN: The count of open parentheses.

   • closedN: The count of closed parentheses.

5. The first if condition checks if we have reached the desired count of open and closed parentheses, both equal to n. If so, it means we have formed a valid combination, and it's added to the res slice by joining the stack using strings.Join.

6. Next, there are two if conditions:

   • if openN < n { ... }: This checks if the count of open parentheses is less than n. If true, it appends an open parenthesis "(" to the stack, increments the count of open parentheses, and then calls backtrack recursively. After the recursive call, it "pops" the last element from the stack to backtrack and explore other possibilities.

   • if closedN < openN { ... }: This checks if the count of closed parentheses is less than the count of open parentheses. If true, it appends a closed parenthesis ")" to the stack, increments the count of closed parentheses, and then calls backtrack recursively. It also pops the last element from the stack afterward for backtracking.

7. Finally, the backtrack function is initially called with openN and closedN both set to 0, starting the recursive process to generate valid combinations.

8. The function returns the res slice, which contains all the valid combinations of parentheses.

9. func pop(list *[]string) { ... }: This function is used to remove the last element from a slice of strings. It's a utility function called within backtrack to backtrack and explore other possibilities by removing the last element added to the stack.

In summary, this code uses a recursive backtracking approach to generate all valid combinations of parentheses pairs with a given count n. It maintains a stack to keep track of the currently open and unclosed parentheses and appends and pops elements from it while exploring possibilities. The valid combinations are stored in the res slice and returned as the final result.